Ситуационная задача.
Мастер парашютного спорта прыгает с некоторой высоты и летит, не раскрывая парашюта. Пролетев значительную часть пути, он дергает за кольцо парашюта и последние сотни метров опускается, паря на своем зонте. Как изменяется скорость движения парашютиста и его высота на отрезке времени от начала движения до момента раскрытия парашюта (т.е., во время затяжного прыжка) с течением времени?
Из условия задачи видно, что она относится к классической механике. В этом  разделе физики процесс движения считается полностью описанным, если известны скорость и координата движущегося тела в каждый момент времени. Поэтому возникает сформулированный выше вопрос. Из общих соображений понятно, что с ростом скорости возрастает сопротивление движению и, следовательно, может возникнуть ситуация, когда с некоторого момента скорость тела становится постоянной. Это приводит к следующему вопросу:
разделе физики процесс движения считается полностью описанным, если известны скорость и координата движущегося тела в каждый момент времени. Поэтому возникает сформулированный выше вопрос. Из общих соображений понятно, что с ростом скорости возрастает сопротивление движению и, следовательно, может возникнуть ситуация, когда с некоторого момента скорость тела становится постоянной. Это приводит к следующему вопросу:
 Справедливо ли предположение о постоянстве скорости с некоторого момента при затяжном прыжке?
Справедливо ли предположение о постоянстве скорости с некоторого момента при затяжном прыжке?
Задания, решение которых приводит к решению поставленной задачи.
- Построить математическую модель движения парашютиста.
- Разработать численную (компьютерную) модель процесса и
 провести моделирование одномерного движения парашютиста на этапе до момента открытия парашюта.
провести моделирование одномерного движения парашютиста на этапе до момента открытия парашюта. - Определить, начиная с какого времени после старта скорость парашютиста в затяжном прыжке становится постоянной.
Материалы, необходимые для выполнения заданий.
Исходные данные
 Масса парашютиста Полуобхват грудной клетки
Масса парашютиста Полуобхват грудной клетки
80 кг 0,45 м
Теоретические сведения
 В классической механике основную роль играет второй закон Ньютона: ускорение, с которым движется тело, прямо пропорционально действующей на него силе и обратно пропорционально его массе:
В классической механике основную роль играет второй закон Ньютона: ускорение, с которым движется тело, прямо пропорционально действующей на него силе и обратно пропорционально его массе:
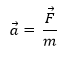
Здесь ![]() — это равнодействующая, т.е. векторная сумма всех сил, действующих на тело. В ситуациях, когда сила или масса не являются постоянными величинами, этот закон имеет более общий вид:
— это равнодействующая, т.е. векторная сумма всех сил, действующих на тело. В ситуациях, когда сила или масса не являются постоянными величинами, этот закон имеет более общий вид:
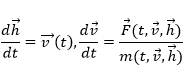
Сила тяжести:![]() , где
, где ![]() – ускорение свободного падения.
– ускорение свободного падения.
Сила сопротивления:![]() .
.
Величина ![]() определяется свойствами среды и формой тела. Например, для шара
определяется свойствами среды и формой тела. Например, для шара ![]() , где
, где ![]() – динамическая вязкость среды,
– динамическая вязкость среды, ![]() – радиус шара. Величина
– радиус шара. Величина ![]() вычисляется как
вычисляется как ![]() , где
, где ![]() – площадь сечения тела, поперечного по отношению к потоку воздуха,
– площадь сечения тела, поперечного по отношению к потоку воздуха, ![]() – плотность среды,
– плотность среды, ![]() коэффициент лобового сопротивления.
коэффициент лобового сопротивления.
При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение:
![]()
При более высоких скоростях сила сопротивления становится пропорциональной квадрату скорости:
![]()
Значения коэффициента лобового сопротивления
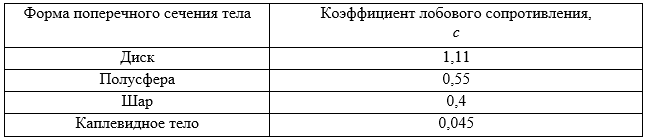
Значения коэффициентов вязкости и плотности веществ
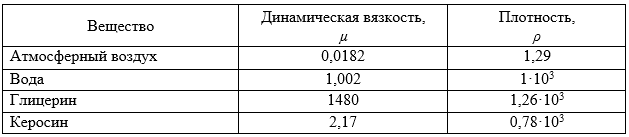
Справочные материалы о программных средствах компьютерного моделирования
 Универсальная система моделирования MVS (Model Vision Studium)
Универсальная система моделирования MVS (Model Vision Studium)
Программные средства для решения задачи.
Универсальная система моделирования MVS скачать
Результаты исследования представьте в виде отчета, который включает:
1) постановку задачи моделирования;
2) формулирование цели и гипотезы исследования;
3) результат построения математической модели;
4) компьютерную модель;
5) описание результатов проведения эксперимента с моделью;
6) проведение анализа результатов, формулирование выводов.
